🧙Creating MAGI: A hard subset of MMLU and AGIEval
Adding Headroom and Discriminative Power to Existing Benchmarks
Fair warning: long article ahead.
[PREVIEW-DRAFT]
⚡TL/DR:
Language model benchmarks are chasing a moving target and rapidly running out of headroom. Popular tests are struggling to effectively separate SOTA models from leaderboard optimisers. Can we salvage these old dinosaurs for scrap and make a better benchmark?
I created two subsets of MMLU + AGIEval:
MAGI-Hard: 5x smaller, 2x more discriminative between top models (as measured by score range) This subset is brutal to 7b models and useful for exposing differences between high ability models. Downside: a reference model (Deepseek-67b) is “burned” and cannot be scored fairly by this subset.
MAGI-IRT: 7x smaller, 1.5x more discriminative. This subset is more balanced and retains discriminative power for low + mid ability models. It uses Item Response Theory (IRT) to model question difficulty, and can score all models fairly.
What’s the takeaway? We can wring more life out of these benchmarks and create smaller versions that are better able to separate the top ability models. These methods can be applied to any test set (or combination of tests) that contain enough hard & discriminative questions.
You can find the MAGI subsets here and use them with this fork of the Eleuther eval harness.
MAGI-Hard has been added as a metric on the EQ-Bench leaderboard.
Motivations for doing this:
Benchmarks are increasingly unable to distinguish between top ability models
Small parameter models (like 7B) are over-fitting benchmarks and overperforming
Easier to remix existing benchmarks than create new ones
Smaller test = cheaper & faster
We need tests that are harder; but a brutally hard test that none of the models can complete is not useful. So, more precisely, we need more discriminative tests.
It’s no trivial thing to construct test questions from scratch to meet these criteria. Fortunately, existing benchmarks like MMLU contain a *lot* of questions, and we can curate a fraction of them with more desirable properties.
Here are some ways we can model question difficulty & discriminative power:
📊Ranking Questions by Average Score
This straightforward approach gives a reasonable approximation for difficulty but it doesn’t differentiate between hard vs discriminative questions. In practice, this heuristic leads to “bad” questions being over-represented in the final set. Bad in the sense that they’re too hard, wrong or misleading. This advantages the weakest models that guess randomly.
Ranking questions by average score gained us a modest 1.2x increase in discriminative power between top models. I measure this by calculating the score range of the top 20% of models tested in this evaluation. We can do a lot better than this!
High Ability Reference Model 🆚 Average of Other Model Scores
This method I refer to herein as Ref-vs-others. It’s something I tried out on a whim and which turned out to be the most discriminative by a large margin.
Ref-vs-others works like this: Choose a high ability reference model, then rank each question by
[reference model score] minus [average of other models’ scores]And then delete 80-90% of the questions that scored lowest on this metric. This approach yielded a 2x increase (!) in range of the top 20% scores over baseline.
Ref-vs-others neatly sidesteps the problems of the average score method – over-representing too-hard or badly designed questions – since we’re discarding all questions that our reference model got wrong.
There is a significant downside to this approach, which is that you cannot score the reference model fairly on the resulting subset. This is because we have selected questions that the reference gets correct. If this tradeoff is not suitable for your use case, you can instead use the MAGI-IRT subset which doesn’t suffer from this issue, but yields about half the gain in discriminative power at the top ability range.
For the MAGI-Hard subset I used Deepseek-67B as the reference model, because it’s a strong model but not currently widely used for fine-tuning. More on this in the Choosing a Reference Model section of the footnotes.
📐Item Response Theory (IRT)
IRT is a widely used and established method in test design. It uses some fancy math to model things like: Respondent ability level, question difficulty, discrimination and guessing.
Using IRT to rank questions yielded a ~1.5x increase in score range of the top models over baseline. An advantage of IRT over Ref-vs-others is that it doesn’t use a reference model to determine question difficulty, so all the models involved in the analysis can still be fairly scored on the final subset.
In addition to deleting the easy questions, I found that deleting ~25% of the hardest questions as ranked by IRT yielded a better final set. Most likely for the same reasons we see good results with Ref-vs-others, which deletes all the questions that the reference model got wrong.
It’s a bit counter-intuitive but it seems that getting rid of the very hardest questions makes for a more discriminative set; we are constraining the subset to questions that are hard but answerable.
Each of these approaches involves tradeoffs and compromises. In the end I created two subsets: one using Ref-vs-others because of that sweet 2x, and one using IRT as a more balanced subset which retains discriminative power in the low-mid range. Let’s get into the deets!
Creating the Hard Subset with Ref-vs-Others
Data collection: Run various benchmarks with Eleuther lm-eval on a set of representative models, recording all answers.
Pick a strong model to be the reference.
Rank the questions by:
[Reference model score] minus [voter models avg. score]Progressively delete questions that score lowest on this metric.
Recalculate scores using the refined subset.
Applying this heuristic, we are left with a subset that includes questions that the reference model got right but others found difficult.
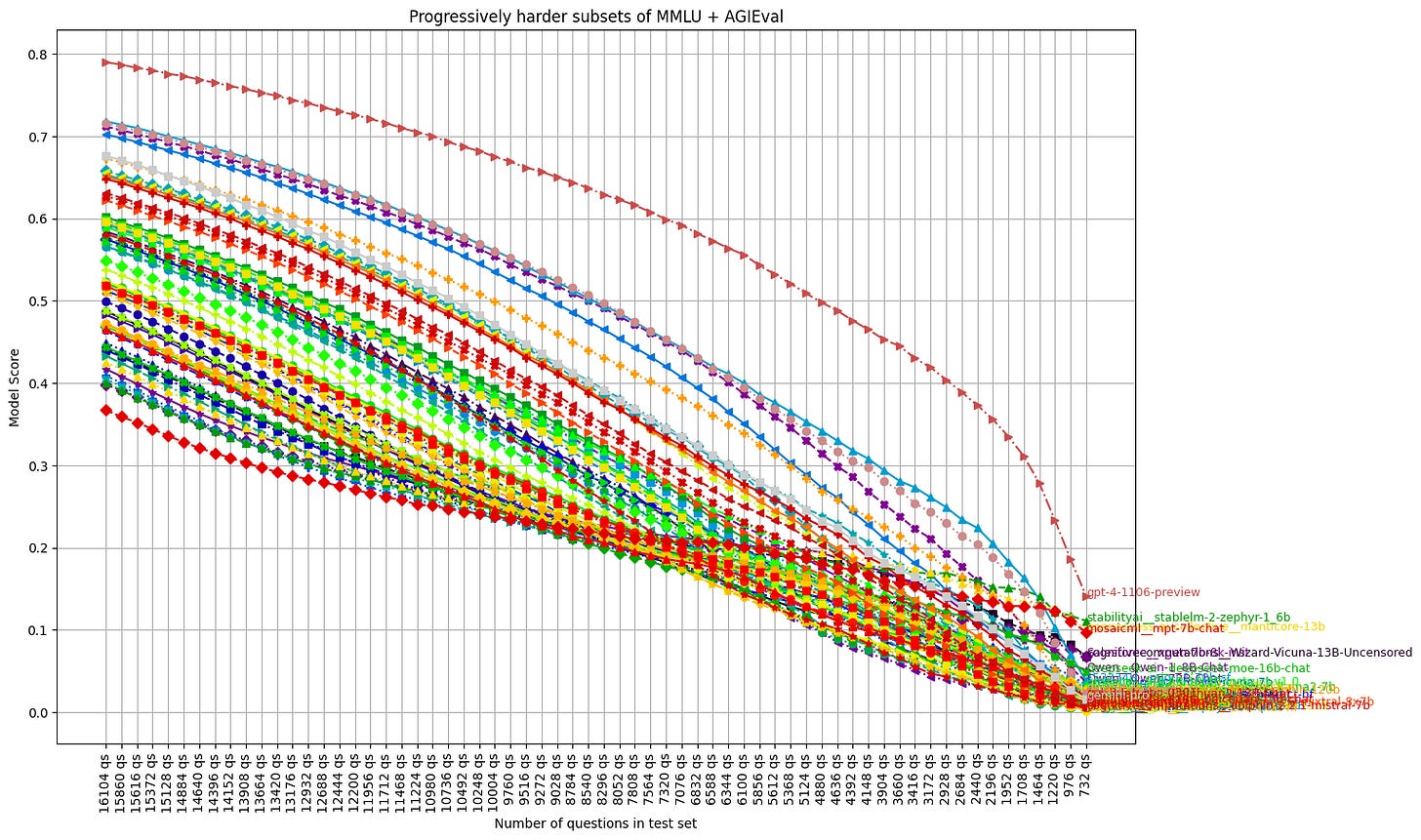
Here is what the score trends looks like for MMLU + AgiEval, as we progressively delete questions (click to zoom):
Explanation of the chart
This is a busy chart with a lot of interesting stuff going on, so let’s break it down.
First, we’ve ordered the test set by our Ref-vs-others metric. Then, we are iteratively deleting chunks of the test set, recalculating scores each time. The x-axis ostensibly represents progressively harder / more discriminative sets of questions. The last point on the x-axis is our final subset of questions (we’ll tweak it a little more from here).
Interpretation
Of immediate interest are the score trends. We can see how the different models respond to the hardest questions. There are “corrections” which reveal the models’ ability to handle really tough questions. Yi-34B for example, which overperforms on MMLU for its parameter size, trends down hard at the end. The 120b MegaDolphin model uptrends at the end, indicating that the higher parameter count of this merged model may confer an advantage to complex reasoning.
It’s a bit hard to tell on this chart, but models typically trend in the direction of parameter size, relative to each other, which results in a number of switched places in the rankings. The hardest subsets are pretty brutal to 7b models.
There is a separation of Miqu and mistral-medium towards the hardest subsets which is very curious. One speculative interpretation could be that Miqu, the leaked 70b MistralAI prototype, is larger than mistral-medium. Or perhaps we are observing the effect of training set contamination that was filtered out in the production model.
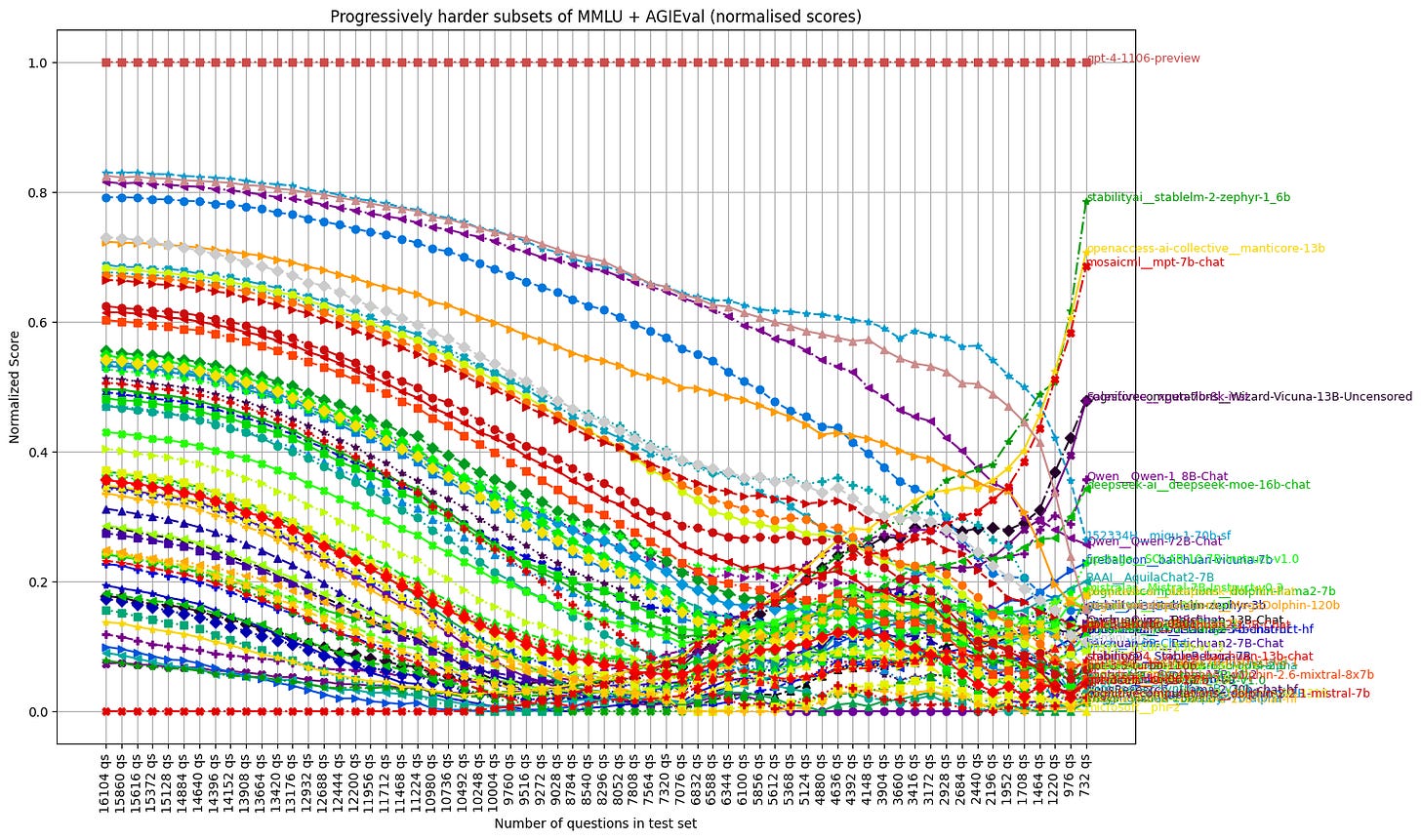
Note that here, the weakest models like zephyr-1_6b are advantaged in the final subset (they trend up at the end above gpt-3.5). This is because we are selecting for questions that most models get wrong, which after a point pushes the average scores below the random baseline (of ~20-25%), which gives guesser models an advantage. Not ideal! But don’t worry, we will fix this.
Introduced Biases
Deleting this much produces some nasty biases and less-than-ideal properties:
Models are scoring below the random baseline
Weak guesser models outperforming stronger models
Voter penalty
We’re going to have to address all of these for the subset to be fairly usable for a leaderboard.
⚠️Voter Penalty
This method (and also IRT) creates a bias against the voter models that were included in the others pool in the Ref-vs-others calculation. I call them “voter models” because they effectively vote on which questions are hard.
Voter penalty is defined as:
[Model x's score when excluded from the analysis] minus [Model x's score when included]Scores are lower for included models. The penalty occurs because we are deciding which questions to include in the final subset by selecting ones that our voter models in particular got wrong. This naturally causes the score for voter models to be lower than if they were not included in the analysis. That’s not cool! We want our test set to be fair.
Ordinarily when this kind of technique is applied to create subsets of e.g. school exams, we wouldn’t care about this bias because the resulting test is not going to be re-taken (and answered exactly the same) by the same students whose scores were used in the analysis. But, here we do want all the participating models to be fairly scored on the final subset. which complicates things a little.
This bias can be partly mitigated by including more (and more diverse) voters in the analysis. We want to choose questions that are generally hard, not ones that are only hard for our voter models specifically.
I estimate the voter penalty per model by running the whole analysis with each model included vs. excluded and comparing the scores.
With just one voter model, the score penalty is ~35 pts (out of 100). With 60 voters we have an average penalty of 1.6 pts, beyond which we see diminishing returns, and are running out of foundational models besides.
By adding a lot of voter models we’ve mitigated the voter penalty to an extent, but some issues remain:
Voter penalty is still significant (~1.6 pts) which is not terrible but also not very fair.
Many models are scoring below the random baseline of ~25%
Random guessers outperform stronger models
Reducing the Voter Penalty with Offset Padding Q’s
The solution I came up with to reduce the voter penalty was, I think, a little inelegant but functional. The idea is that we can re-add previously deleted questions in a targeted way, choosing questions that the voter models got right. This offsets the unfairness of their being discriminated against in the initial voting & deletion process.
Handily, this also mitigates issues 2 & 3 by bringing up the scores of the lower ability models so they are above the random baseline, meaning random guessers are no longer advantaged.
I spent a lot of time experimenting with different ways to pad the test set with previously deleted questions to reduce the voter penalty. The condensed version of which is that I iteratively added random questions that each voter model got right, per model, the number of which was proportional to that model’s voter penalty. More in the footnotes if you want the full scoop.
Here’s a chart of the voter penalties per model before & after offset padding:
These are the score trends with offset padding included:
The purple arrows indicate the increase in spread for the top model scores.
The parameters I optimised for here placed a high importance on discriminative power between the top models. This effectively has squashed the scores of the mid to low ability models into a small range. This tradeoff is fine for my purposes as I wanted the MAGI-Hard set primarily to add headroom to the EQ-Bench leaderboard.
If you prefer not to squash the low and mid ability model scores so much, the MAGI-IRT subset is more balanced.
🎉The End Result
The final MAGI-Hard set is 3203 questions, a 5x reduction over the original set. It is 2x more discriminative amongst the top models tested (measured by range of the top 20% of scores), which represents a steep hill to climb for those aspiring 7b leaderboard optimisers.
The MAGI-IRT set contains 2154 questions. It’s more useful for everyday benchmarking over a range of ability levels.
Further Work
There may be some improvements that can be made with different IRT implementations or parameters, or other novel ways of modelling question difficulty. I’m far from an expert in test theory so there are no doubt some gains to be made with the question selection process. Intuitively I feel there ought to be a way to get near the discriminative power of Ref-vs-Others without requiring a sacrificial reference model.
Auditioning a wider range of benchmarks for possible inclusion would be a worthwhile endeavour. In theory, tens/hundreds of benchmarks could be combined and the ultimate discriminative subset chosen from them.
Since Ref-vs-others screens out questions that the reference model got wrong, we are effectively limiting our question pool (and thus the headroom of the benchmark) to those the reference model could answer correctly. As more powerful models are released, it would make sense to create new subsets using stronger models as the reference.
Finally: If anyone is interested in the code for generating these subsets, it’s currently a mess of ipynb, but I can & will sort it out. Hit me up.
Citations
Paech, S. J. (2023). EQ-Bench: An Emotional Intelligence Benchmark for Large Language Models. arXiv preprint arXiv:2312.06281. Available at arXiv:2312.06281.
Lord, F. M. (2012). Applications of item response theory to practical testing problems. Routledge.
Hendrycks, D., Burns, C., Basart, S., Zou, A., Mazeika, M., Song, D., & Steinhardt, J. (2021). Measuring Massive Multitask Language Understanding. Proceedings of the International Conference on Learning Representations (ICLR).
Hendrycks, D., Burns, C., Basart, S., Critch, A., Li, J., Song, D., & Steinhardt, J. (2021). Aligning AI With Shared Human Values. Proceedings of the International Conference on Learning Representations (ICLR).
Zhong, W., Cui, R., Guo, Y., Liang, Y., Lu, S., Wang, Y., Saied, A., Chen, W., & Duan, N. (2023). AGIEval: A Human-Centric Benchmark for Evaluating Foundation Models. arXiv preprint arXiv:2304.06364. Available at arXiv:2304.06364.
Ling, W., Yogatama, D., Dyer, C., & Blunsom, P. (2017, July). Program Induction by Rationale Generation: Learning to Solve and Explain Algebraic Word Problems. Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Vol. 1, pp. 158-167). Vancouver, Canada: Association for Computational Linguistics. https://doi.org/10.18653/v1/P17-1015.
Hendrycks, D., Burns, C., Kadavath, S., Arora, A., Basart, S., Tang, E., Song, D., & Steinhardt, J. (2021). Measuring Mathematical Problem Solving With the MATH Dataset. NeurIPS.
Liu, J., Cui, L., Liu, H., Huang, D., Wang, Y., & Zhang, Y. (2020). LogiQA: A Challenge Dataset for Machine Reading Comprehension with Logical Reasoning. International Joint Conference on Artificial Intelligence.
Zhong, H., Xiao, C., Tu, C., Zhang, T., Liu, Z., & Sun, M. (2020). JEC-QA: A Legal-Domain Question Answering Dataset. Proceedings of AAAI.
Wang, S., Liu, Z., Zhong, W., Zhou, M., Wei, Z., Chen, Z., & Duan, N. (2021). From LSAT: The Progress and Challenges of Complex Reasoning. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 30, 2201-2216.
📜Footnotes:
I cut a lot of detail out of the main article; the remainder is for those who wish to reproduce the method or who are otherwise masochistic chart junkies:
Why do the scores trend up then down?
The initial uptrend happens because the Ref-vs-others heuristic orders questions that our reference model got wrong first. So these questions (which are mostly difficult ones, since our reference model got them wrong) get deleted first, causing that uptick in the scores.
The downtrend begins when we hit the questions that our reference model got correct. From here, we are initially deleting questions that almost every model got right. As the series progresses we delete progressively harder questions until we are left with a small subset.
Parameter Optimisation for Voter Penalty Offset Questions
That’s a bit of a mouthful. So to recap, we are trying to offset the score penalty for models that were included in the analysis (voter penalty) by re-adding questions that benefit the voter models.
Various selection methods & parameter ranges were explored, including:
Percent of the original test set deleted
Different ways of ordering the candidate padding questions (I went with avg. score)
The ranges of the candidate questions to select from:
Hard questions reduce the voter penalty but don’t increase average score or address guesser advantage
Easy questions increase the average score but reduce discriminative power between top models
The number of padding questions selected for each range
Using Bayesian optimisation over these parameters, the following metrics were optimised for:
Standard deviation of the top 10 model scores (higher is better)
Average voter penalty (lower is better)
Minimum score (should be >= 25)
Guesser advantage (random guessers are advantaged over non-guessers; lower is better)
Size of test set (lower is better)
An optimised test set was computed with these properties:
Std. dev. of top 10 models: 0.083 (vs 0.02 in the original set)
Average voter penalty: 0.43 (out of 100)
Continuing the story of compromises and tradeoffs: these optimisation metrics were in competition so we lost some discriminative power by reducing the voter penalty, and so forth. But the end result is an average voter penalty that I can live with (0.43), and a healthy 4x increase in std. dev. between the top model scores.
Item Response Theory (IRT)
I used py-irt to compute the discrimination & difficulty coefficients for each question. I used the 2 parameter model, as the others produced worse results. It’s possible there may be ways to get better results; this is my first time doing IRT analysis so it’s quite possible I did this sub-optimally.
Here are the score trends when using IRT.
Deletion candidates sorted by question difficulty as determined by IRT:
Deletion candidates sorted by question discrimination as determined by IRT:
The IRT trends are more sedate than Ref-vs-others. The score disparities between the top models are less pronounced and we’re not seeing so much of the interesting corrections that we get with Ref-vs-others. The fact that IRT-difficulty produced the mildest effects (though still “working” in the sense that average score goes down) was surprising. It’s possible the IRT analysis hasn’t worked as well as it should have; someone with more familiarity with IRT might be able to do a better job here.
Note: the uptrend at the end is due to the offset padding questions having a stronger impact as the question set size decreases.
Ranking by Average Score
More of these wacky charts. This time showing the score trends when we are modelling question difficulty by the average score of all voter models.
The normalised chart in particular illustrates the effect of guesser advantage.
Choosing source benchmarks
Source benchmarks need to contain sufficient hard & discriminative questions in them for this method to be effective. As it turned out, most of the common ones (at least, that I tested) didn’t contain enough discriminative questions to be worth the time.
I generated data for:
Bigbench (hard), AGIEval, MMLU, Hellaswag, Winogrande, BoolQ, OpenbookQA and Piqa.
To decide which benchmarks to include, I looked at the score trend charts to see if the top models showed significantly more spread in the hardest subsets. I also looked at some objective metrics; primarily the std. dev. of the top model scores, to gauge how well they could discriminate between the very top models once pared down.
I’ll spare you more charts, but MMLU and AGIEval were by far the best. I had thought Bigbench (hard) would be a good candidate, but in actuality it contains a lot of unnecessarily large categories full of repetitive, too-hard synthetic questions. Hellaswag nearly made the cut, but in the end it was not offering enough discriminative value per questions added.
I did go through the charts for MMLU and AGIEval per category which was quite revealing. Certain categories like Moral Disputes in MMLU are very discriminative. Something I will keep in mind when designing future tests.
Choosing a reference model
The reference model in Ref-vs-others can’t be fairly scored, since we’ve selected for questions that it answered correctly. I picked Deepseek-67B because it’s a strong model, so will be effective at determining which questions are hard but answerable. This Deepseek model is not widely used for fine-tuning compared to other leading open models, so it became the sacrificial lamb in the creation of MAGI-Hard.
Needing to “burn” the reference model (and its fine-tunes) is a significant drawback of the Ref-vs-others method. Using IRT to select questions avoids this, but it produces a final set which is significantly less discriminative.
It’s a trade-off and you can select which approach makes more sense for your use-case. In some applications it may make more sense to use MAGI-IRT which doesn’t favour any model or require specific knowledge to deploy fairly.
Discussing Biases
I’ve done my best to minimise and mitigate potential biases introduced by the subset selection process. Having run MAGI-Hard on the full set of models on the EQ-Bench leaderboard, most of which were not included in this analysis, none stand out as being clearly advantaged or disadvantaged other than corrections in the direction of parameter size. Which is to say: Out-of-distribution models score sanely, by my reckoning.
Deepseek-67b, the chosen reference model, scores 78.6 on the final MAGI set. This result should be considered invalid given the strong selection bias in favour of the reference model. It’s 🔥 burned. Do not use. (sorry Deepseek-ai).
To gauge whether using Deepseek-67b as the reference model has advantaged others in the same family, I benchmarked some other Deepseek models:
deepseek-ai/deepseek-coder-7b-instruct-v1.5
MAGI-Hard Score: 29.53
deepseek-ai/deepseek-llm-7b-chat
MAGI-Hard Score: 31.10
deepseek-ai/deepseek-coder-33b-instruct
MAGI-Hard Score: 24.23
Based on these results it appears there is no strong bias advantaging these other deepseek models. They are all scoring quite low.
Guesser Models
These are weak models that answer randomly more often than not.
I identified and removed guesser models from the analysis (although I still left them in the chart). They are not good voters for determining which questions are difficult & discriminative.
Ablation studies of different reference models
Of the reference models tested with Ref-vs-others, I tried GPT-4, Qwen-72b-chat, Deepseek-72b and Yi-34b-chat. Deepseek-72b produced the best discriminative power out of these. I explored using multiple models as reference, and it works, but doesn’t give any advantage in discriminatory power, and it also makes more models unusable for testing with the final subset.
I initially assumed I ought to be using the strongest model as the reference (GPT-4), and that this would make the test more discriminative of the very top end of the ability range. The reasoning being that all the questions that the reference model got wrong get deleted, so, stronger reference = more hard questions in the final set. However, contrary to expectations, other reference models performed similarly or better. It would be interesting to try using mid-range 7b models to create a subset which is more discriminative between the lower ability ranges. If we need more headroom in the future, we can regenerate the subset using new, stronger SOTA models.
Choosing voter models:
I aimed to include 3 representative chat- or instruct-tuned models from every major foundational model + param size variant. Choosing more representatives of a given base model would have increased the voter penalty for other fine-tunes of that base model, because they will have similar answering patterns. Choosing fewer representatives per base model increases the average voter penalty. I just followed my nose with this part; further work could look at optimising the voter model selection. The final set included 66 voter models:
01-ai/Yi-34B-Chat
01-ai/Yi-6B-Chat
152334H/miqu-1-70b-sf
BAAI/AquilaChat2-7B
HuggingFaceH4/zephyr-7b-alpha
Intel/neural-chat-7b-v3-1
NousResearch/Llama-2-13b-chat-hf
NousResearch/Llama-2-70b-chat-hf
NousResearch/Llama-2-7b-chat-hf
OpenAssistant/llama2-13b-orca-8k-3319
Qwen/Qwen-14B-Chat
Qwen/Qwen-1_8B-Chat
Qwen/Qwen-72B-Chat
Salesforce/xgen-7b-8k-inst
WizardLM/WizardLM-70B-V1.0
YeungNLP/firefly-qwen-7b
allenai/tulu-2-dpo-70b
baichuan-inc/Baichuan-13B-Chat
baichuan-inc/Baichuan2-13B-Chat
baichuan-inc/Baichuan2-7B-Chat
berkeley-nest/Starling-LM-7B-alpha
codellama/CodeLlama-34b-Instruct-hf
cognitivecomputations/MegaDolphin-120b
cognitivecomputations/Wizard-Vicuna-13B-Uncensored
cognitivecomputations/dolphin-2.2.1-mistral-7b
cognitivecomputations/dolphin-2.6-mixtral-8x7b
cognitivecomputations/dolphin-llama2-7b
deepseek-ai/deepseek-llm-67b-chat
deepseek-ai/deepseek-llm-7b-chat
deepseek-ai/deepseek-moe-16b-chat
fireballoon/baichuan-vicuna-7b
gemini-pro
gpt-3.5-turbo-0301
gpt-3.5-turbo-0613
gpt-3.5-turbo-1106
gpt-4-1106-preview
jondurbin/airoboros-65b-gpt4-2.0
llmware/dragon-yi-6b-v0
lmsys/vicuna-13b-v1.3
lmsys/vicuna-13b-v1.5
lmsys/vicuna-33b-v1.3
lmsys/vicuna-7b-v1.3
lmsys/vicuna-7b-v1.5
lxuechen/phi-2-dpo
microsoft/Orca-2-7b
microsoft/phi-2
migtissera/SynthIA-70B-v1.5
migtissera/Synthia-13B-v1.2
migtissera/Synthia-7B-v3.0
migtissera/Tess-XL-v1.0
mistral-medium
mistralai/Mistral-7B-Instruct-v0.1
mistralai/Mistral-7B-Instruct-v0.2
mistralai/Mixtral-8x7B-Instruct-v0.1
mosaicml/mpt-30b-chat
mosaicml/mpt-7b-chat
openaccess-ai-collective/manticore-13b
openchat/openchat_3.5
rhysjones/phi-2-orange
senseable/WestLake-7B-v2
shibing624/vicuna-baichuan-13b-chat
stabilityai/StableBeluga-7B
stabilityai/stablelm-2-zephyr-1_6b
stabilityai/stablelm-zephyr-3b
teknium/OpenHermes-2.5-Mistral-7B
upstage/SOLAR-10.7B-Instruct-v1.0